高中数学双曲线公式总结大全（掌握双曲线公式）

高中数学中，双曲线是一个重要的概念。掌握双曲线的公式是解决各种与双曲线相关的问题的基础。本文将高中数学中常见的双曲线公式，帮助读者更好地理解和运用这一知识点。

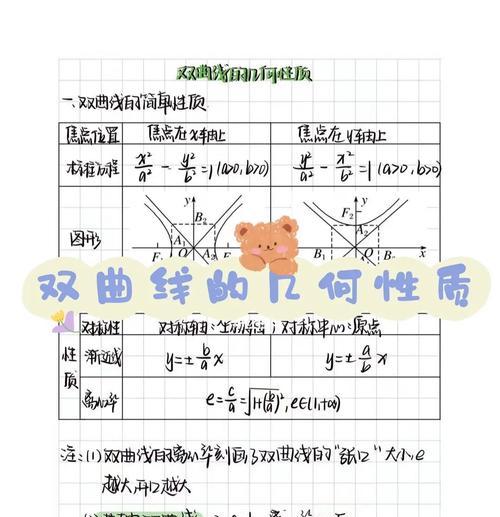
一、双曲线的基本定义和性质

在本节中，将介绍什么是双曲线以及双曲线的基本性质。双曲线的定义、焦点、准线等概念将一一详细解释，帮助读者对双曲线有更深入的理解。

二、标准方程与一般方程的转换

本节将介绍双曲线的标准方程和一般方程之间的相互转换。通过学习这一转换方法，读者可以更灵活地应用不同形式的方程来解决问题。

三、双曲线的焦点和准线位置关系

本节将讨论焦点和准线在双曲线上的位置关系。通过分析焦点和准线的相对位置，读者可以更好地理解双曲线的几何性质，并在解题过程中运用这一关系。

四、双曲线的离心率与形状关系

离心率是描述双曲线形状的一个重要指标。本节将介绍离心率与双曲线的形状之间的关系，并通过实例演示如何根据离心率确定双曲线的形态。

五、双曲线的渐近线与渐近点

双曲线具有渐近线和渐近点，它们在解题过程中起到重要的辅助作用。本节将详细介绍渐近线和渐近点的定义和求法，并解释它们在数学问题中的应用。

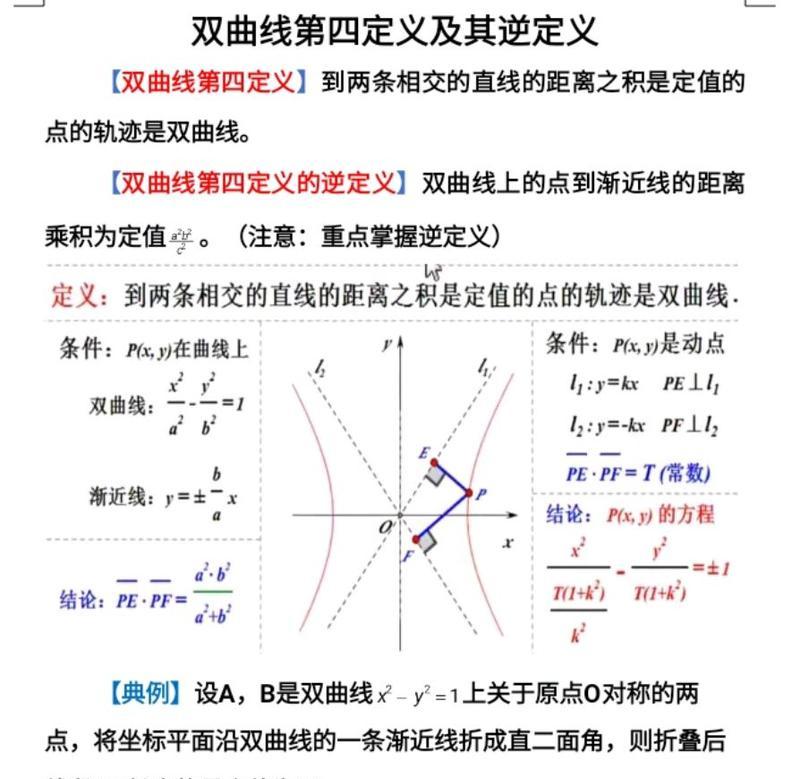
六、双曲线的对称性与坐标变换

本节将探讨双曲线的对称性及其与坐标变换之间的关系。通过了解双曲线的对称性，读者可以更加方便地进行坐标变换，简化问题的求解过程。

七、离散点与连续函数双曲线的特殊性质

除了常规的双曲线，本节将介绍离散点和连续函数双曲线的特殊性质。了解这些特殊双曲线的性质，可以帮助读者更好地应对各类数学题目。

八、双曲线与其他数学概念的关联

在本节中，将讨论双曲线与其他数学概念之间的关联。双曲线与椭圆、抛物线等曲线的联系，以及与指数函数、对数函数等函数的关系都将在此介绍。

九、双曲线的应用举例

本节将通过一些实际问题的应用案例，展示双曲线公式在实际问题中的运用。通过具体的例子，读者可以更好地理解和掌握双曲线公式的应用方法。

十、思维拓展：双曲线的更多应用

本节将引导读者进一步思考双曲线的应用领域，并提供一些扩展性的问题，帮助读者深入思考和拓展对双曲线的理解。

十一、掌握双曲线公式，轻松应对高中数学

通过对本文内容的阅读和理解，读者可以系统性地掌握双曲线公式，并能够灵活运用于各种相关问题的求解中。掌握双曲线公式不仅可以帮助读者提高数学成绩，还能够在日常生活中应用数学思维解决问题。

双曲线是高中数学中的重要知识点，掌握其公式是解决与双曲线相关问题的基础。通过本文的系统和详细讲解，读者可以更好地理解和应用双曲线公式，提高数学水平。