探究电脑函数的最大值最小值公式（函数求极值的关键方法及应用）

在数学中，求函数的最大值和最小值是一个重要的问题，它在各个领域都有广泛的应用。随着计算机的发展，我们可以利用电脑来快速求解函数的最大值和最小值，从而大大提高计算效率。本文将以电脑函数最大值最小值公式为主题，介绍函数求极值的关键方法及其应用。

一、确定函数求极值的条件

二、利用导数法求解函数的极值

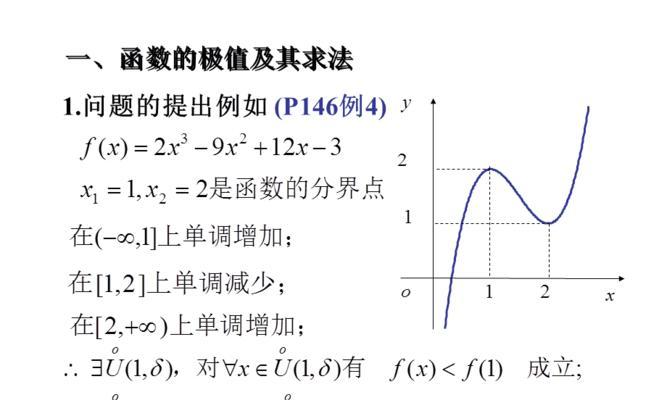
三、利用二阶导数法求解函数的极值

四、利用离散点法求解函数的极值

五、利用穷举法求解函数的极值

六、利用遗传算法求解函数的极值

七、利用优化算法求解函数的极值

八、利用约束条件求解函数的极值

九、利用动态规划求解函数的极值

十、利用神经网络求解函数的极值

十一、利用模拟退火算法求解函数的极值

十二、利用蚁群算法求解函数的极值

十三、利用遗传编程求解函数的极值

十四、利用辅助函数求解函数的极值

十五、利用图形化方法求解函数的极值

确定函数求极值的条件

确定函数求极值的条件是解决函数最大值和最小值问题的第一步，只有满足一定的条件，我们才能使用相应的方法来求解。常见的条件包括函数在一定区间内连续、可导以及存在临界点等。

利用导数法求解函数的极值

导数法是求函数极值的常用方法，我们可以通过计算函数的导数，找到导数为零的点，进而确定函数的最大值和最小值。这种方法在实际应用中具有广泛的适用性和高效性。

利用二阶导数法求解函数的极值

二阶导数法是导数法的一种改进，通过计算函数的二阶导数，我们可以判断函数在某点处的凸凹性以及极值点的存在性。这种方法对于特殊的函数形式或者需要更精确的结果时往往更有效。

利用离散点法求解函数的极值

离散点法是一种基于计算机的数值计算方法，通过在函数的定义域内取一系列离散的点，然后计算函数在这些点处的取值，从而得到函数的最大值和最小值。这种方法对于复杂函数或者缺乏解析表达式的函数往往更为适用。

利用穷举法求解函数的极值

穷举法是一种简单但有效的方法，它通过在函数的定义域内按照一定的步长取样，然后计算函数在每个取样点处的取值，从而找到函数的最大值和最小值。尽管这种方法计算量大，但在一些特殊情况下仍然有其独特的优势。

利用遗传算法求解函数的极值

遗传算法是一种模拟生物进化过程的优化算法，通过模拟种群个体之间的交叉、变异和选择等操作，逐步寻找函数的最大值和最小值。这种方法具有较强的全局搜索能力和鲁棒性，在复杂函数优化问题中有着广泛的应用。

利用优化算法求解函数的极值

优化算法是一类常见的数值优化方法，通过设定目标函数和约束条件，利用迭代的方式逐步优化目标函数的值，从而得到函数的最大值和最小值。这种方法通常能够提供较为准确的结果，并且具有较高的计算效率。

利用约束条件求解函数的极值

在实际问题中，往往存在一些约束条件，限制了函数极值的取值范围。我们需要在求解函数极值时考虑这些约束条件，并采用相应的算法来满足约束条件的要求，从而找到满足约束条件下的最大值和最小值。

利用动态规划求解函数的极值

动态规划是一种常用的优化方法，通过将问题划分为子问题，并利用子问题之间的关系来逐步求解，从而得到函数的最大值和最小值。这种方法通常适用于具有重叠子问题结构和最优子结构性质的问题。

利用神经网络求解函数的极值

神经网络是一种模拟人脑神经元工作方式的计算模型，它通过学习输入和输出之间的映射关系，从而预测函数的最大值和最小值。这种方法在函数拟合和非线性优化问题中有着广泛的应用。

利用模拟退火算法求解函数的极值

模拟退火算法是一种基于随机搜索的全局优化方法，通过模拟固体物体在高温下退火过程中的原子运动，逐步搜索函数的最大值和最小值。这种方法具有较好的全局搜索能力和鲁棒性。

利用蚁群算法求解函数的极值

蚁群算法是一种模拟蚂蚁觅食行为的优化算法，通过模拟蚂蚁在环境中的行为选择和信息交流，逐步寻找函数的最大值和最小值。这种方法对于复杂函数和多峰函数的优化问题有着良好的适应性。

利用遗传编程求解函数的极值

遗传编程是一种利用进化计算思想解决函数优化问题的方法，通过不断迭代和演化，逐步改进个体的表达能力和适应度，从而求解函数的最大值和最小值。这种方法适用于问题复杂、解空间大的情况。

利用辅助函数求解函数的极值

在实际问题中，我们往往可以通过构造辅助函数来简化函数的求解过程，从而更快速地找到函数的最大值和最小值。这种方法需要依据具体问题选择合适的辅助函数，并结合相应的求解方法进行求解。

利用图形化方法求解函数的极值

图形化方法是一种直观、直接地求解函数极值的方法，通过绘制函数的图像，我们可以观察到函数的变化趋势和特点，从而找到函数的最大值和最小值。这种方法常用于教学和初步分析中，能够帮助我们直观地理解函数的性质。

本文介绍了以电脑函数最大值最小值公式为主题的文章，从多个角度讨论了函数求极值的关键方法及其应用。通过利用不同的算法和技术，我们可以快速、准确地求解函数的最大值和最小值，为实际问题的求解提供了重要的工具和思路。同时，我们也意识到在不同场景下选择合适的方法至关重要，只有充分发挥电脑的计算能力和算法的优势，才能更好地解决函数求极值的问题。