以高中数学求最小值的方法（从优化问题到最值定理，探究数学中求最小值的技巧和方法）

求解最小值是一个常见的问题，在高中数学中。从而解决实际生活中的各种问题、通过优化问题和最值定理等数学方法，我们可以找到函数或方程的最小值。帮助读者深入理解和应用这些技巧，本文将探究以高中数学求最小值的方法。

优化问题的引入

我们常常需要找到一种的解决方案或策略，在实际问题中。而求最小值就是解决优化问题的一种方法。我们可以通过高中数学知识来求解最小值，通过研究问题本身，将其转化为数学模型。

函数的极值点

函数的极值点是函数在某个区间内取得或最小值的点。通过求导可得到函数的极值点。从而找到函数的最小值，当导数为零或不存在时，我们可以得到函数的极值点。

一元二次函数的最小值

我们可以使用完全平方式来求解其最小值、对于一元二次函数。我们可以得到最小值的坐标和最小值点的横坐标，通过将函数转化为标准形式。

最值定理的应用

它给出了函数在闭区间上的值和最小值一定存在、最值定理是高中数学中的一个重要定理。我们可以在一定范围内求解函数的最小值，并得到最小值点的坐标，通过使用最值定理。

利用微积分求解最小值

我们可以求解一些复杂函数的最小值、利用微积分的概念和方法。我们可以确定函数的最小值，通过求导，判断函数的单调性和极值点，并进一步应用于实际问题中。

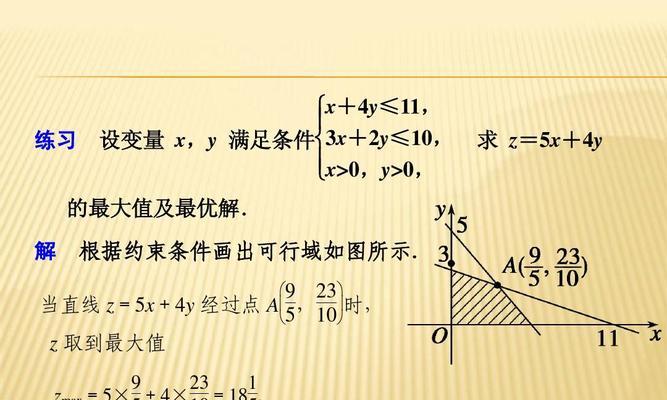
约束条件下的最小值问题

往往会存在一些约束条件，在实际问题中。我们可以求解带有约束条件的最小值问题，从而找到最优解，通过建立含有约束条件的数学模型。

最小二乘法及其应用

在实际问题中被广泛应用、最小二乘法是一种常见的拟合方法。并找到一条拟合曲线、我们可以得到函数的最小值，通过最小化误差平方和。

线性规划中的最小值问题

通过线性函数和线性不等式建立数学模型，线性规划是运筹学中的重要分支、从而得到最优解，我们可以求解出线性规划问题中的最小值。

向量法求解最小值

通过最小化向量的模长或者点乘结果来求解最小值，我们可以运用向量的性质和定理，对于包含向量的数学问题，进而得到问题的解决方案。

隐函数求解最小值

方程可能无法显式表达出来，这时候我们可以使用隐函数的方法来求解最小值，某些问题中。我们可以得到隐函数的最小值、通过求偏导数和利用约束条件。

二次剩余定理及其应用

它与最小值问题有着密切关系，二次剩余定理是数论中的重要定理。我们可以求解一些复杂方程的最小值、通过运用二次剩余定理。

使用软件工具求解最小值

我们可以利用各种数学软件工具来求解最小值问题、在现代科技的支持下。这些软件可以快速地计算出函数的最小值，通过输入函数或方程。

最小值问题在实际生活中的应用

最小值问题在实际生活中有着广泛的应用。最优化设计和资源分配等领域、我们都需要求解最小值问题来得到方案，在最短路径问题。

数学思维在求解最小值问题中的重要性

通过建立数学模型，我们可以找到函数或方程的最小值，运用定理和方法，求解最小值问题需要灵活运用数学思维。这种思维方式培养了我们的逻辑思维和问题解决能力。

我们了解了以高中数学求最小值的方法，通过本文的介绍。利用最值定理、无论是求导，线性规划还是使用软件工具、这些方法都可以帮助我们解决实际生活中的问题。还有助于培养我们的思维方式和解决问题的能力、求解最小值不仅能够提升我们的数学能力。解决更多的实际问题，让我们在今后的学习和应用中充分发挥数学的力量。