虚数的绝对值如何计算？虚数绝对值的定义是什么？

虚数作为复数的一部分，在数学领域中起着重要的作用。虚数的绝对值是一个常见但却具有一定难度的问题，本文将深入探讨虚数绝对值的计算方法及其背后的数学原理。

什么是虚数？

复数与虚数的关系

虚数绝对值的定义

纯虚数的绝对值计算方法

一般复数的绝对值计算方法

欧拉公式与虚数的绝对值

虚数绝对值的几何意义

应用案例：电路中的虚数与绝对值

复数平面中的虚数绝对值

三角形与虚数绝对值的关系

复数运算与虚数绝对值

复数方程中的虚数绝对值

复数函数与虚数绝对值

实际应用中的虚数绝对值问题

探索虚数绝对值的无限魅力

什么是虚数？

在数学中，虚数是指具有形式为bi的数，其中b是实数且i是虚数单位。虚数单位i定义为i2=-1，它是一个无法通过实数表示的数。虚数的引入使得复数的概念更加完整，并且在许多领域中都有重要的应用。

复数与虚数的关系

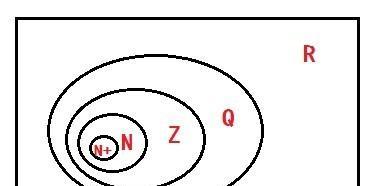
复数是由实部和虚部组成的数。实部是一个实数，虚部是一个虚数。可以将复数表示为a+bi的形式，其中a为实部，b为虚部。虚数可以看作是复数中的一种特殊情况，即实部为0。

虚数绝对值的定义

虚数的绝对值表示虚数与原点之间的距离。根据数学定义，虚数bi的绝对值记作|bi|=|b|。换句话说，虚数的绝对值等于其虚部的绝对值。

纯虚数的绝对值计算方法

纯虚数是指实部为0的虚数。对于纯虚数bi，其绝对值即为|b|。

一般复数的绝对值计算方法

对于一般复数a+bi，可以使用勾股定理来计算其绝对值。即|a+bi|=√(a2+b2)。

欧拉公式与虚数的绝对值

欧拉公式e^(ix)=cos(x)+isin(x)是将虚数与三角函数联系起来的重要公式。利用欧拉公式，可以通过将复数转化为指数形式来计算虚数的绝对值。

虚数绝对值的几何意义

在复数平面中，虚数对应于y轴上的点。虚数绝对值可以视为该点到原点的距离，它在几何上代表了虚数的大小。

应用案例：电路中的虚数与绝对值

在电路分析中，虚数常常用于描述电流和电压之间的相位关系。计算虚数的绝对值可以帮助工程师确定电路中的功率和能量传输情况。

复数平面中的虚数绝对值

复数平面将实部和虚部分别映射到x轴和y轴上，虚数在复数平面中对应于一条与x轴垂直的线。虚数的绝对值即为该线段的长度。

三角形与虚数绝对值的关系

在复数平面中，虚数对应于一个直角三角形，其中斜边的长度就是虚数的绝对值。这种几何关系可以帮助我们更好地理解虚数的概念。

复数运算与虚数绝对值

复数运算中，加法、减法、乘法和除法都会影响虚数的绝对值。了解这些运算规则可以帮助我们更加灵活地计算虚数的绝对值。

复数方程中的虚数绝对值

在解复数方程时，虚数的绝对值往往起到重要的作用。通过计算虚数的绝对值，我们可以得到方程的解集。

复数函数与虚数绝对值

在复数函数中，虚数的绝对值常常用于描述函数的性质。虚数绝对值趋于无穷大时，函数可能趋于发散。

实际应用中的虚数绝对值问题

在物理学、工程学和经济学等领域中，虚数绝对值常常出现在实际问题中。了解虚数绝对值的计算方法可以帮助我们解决这些实际应用中的复杂问题。

探索虚数绝对值的无限魅力

通过本文的介绍，我们可以看到虚数绝对值的计算方法及其背后的数学原理。虚数绝对值在数学和实际应用中都起着重要的作用，它的探索不仅有助于我们理解复数的概念，也展示了数学的无限魅力。