探索根号符号的奥秘（揭开根号符号的用途与运算法则）

经常在各类数学问题中出现，根号符号是数学中常见的一个符号。根号符号仍然是一个神秘的存在，对于许多人来说，然而。帮助读者更好地理解和运用这一数学符号，本文将深入探索根号符号的意义、用途与运算法则。

根号符号的基本概念和表示方法

数学上表示为√a或者√(a)、根号符号以√为表示。它可以是任意实数或者复数，其中a被称为被开方数。根号符号实际上是求解某个数的平方根的操作。

平方根的定义与性质

通常用符号√来表示，平方根是指一个数的平方等于该数的算术平方根。性和加减法性质等特点，平方根具有非负性，这些特性对于后续的根号运算非常重要。

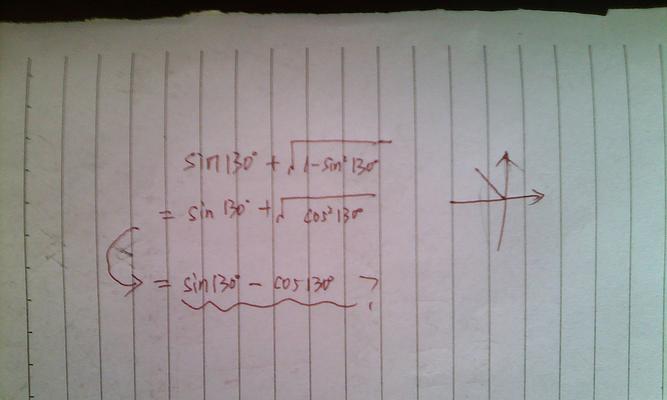
根号运算的基本法则

除法法则和化简法则，根号运算有一些基本的法则，包括乘法法则。乘法法则是指两个数的平方根相乘等于这两个数的积的平方根；除法法则是指两个数的平方根相除等于这两个数的商的平方根；可以将其化简为一个更简单的形式，化简法则是指求解含有多个根号的表达式时。

整数根号运算的特殊性质

根号运算会具有特殊的性质，当被开方数是一个完全平方数时。那么它的根号一定是一个整数，如果一个数是另一个整数的平方、特别地。这个性质在实际问题中有着广泛的应用。

分数根号运算的应用

根号运算可以将其化简为一个更简洁的形式、当被开方数是一个分数时。我们可以简化计算过程并得到更清晰的结果、通过合理运用根号运算的化简法则。这在计算和理解某些复杂问题时非常有用。

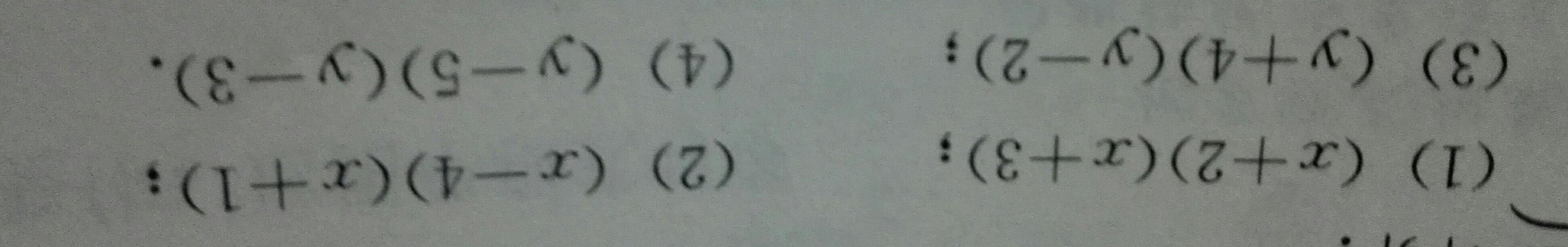
负数根号运算的引入与意义

存在一类特殊的数称为负数，在实数范围内。负数并没有实数范围内对应的平方根、然而。数学家引入了虚数和复数的概念，为了解决这个问题。根号运算在虚数和复数领域中有着重要的应用和意义。

复数根号运算的性质和运算规律

复数根号运算具有一些特殊的性质和运算规律。加减法性质以及乘法法则等都是我们需要理解和掌握的重要内容，复数根号的性。掌握这些规律可以帮助我们在解决复杂问题时更加地进行运算。

根号符号在几何学中的应用

根号符号在几何学中有着广泛的应用。直角三角形的斜边长度以及其他几何形状的边长等，根号可以表示线段长度。深入理解根号符号在几何学中的应用可以帮助我们更好地理解和解决与几何相关的问题。

根号符号在物理学中的应用

根号符号在物理学中也有着重要的应用。速度和加速度之间的关系可以通过根号符号进行表示，在力学中。理解根号符号在物理学中的运用可以帮助我们更好地解决与物理相关的问题。

根号符号在工程学中的应用

根号符号在工程学中常常用于计算和表示某些物理量的大小。压力等工程中常见的物理量，功率，根号符号可以表示电压。了解根号符号在工程学中的应用可以帮助我们更好地理解和应用相关概念。

根号符号的误用与常见错误

但由于其特殊性质和运算规律，容易引起一些误用和常见错误，尽管根号符号在数学中有着广泛的应用。或者将负数直接进行根号运算等、在化简表达式时忽略根号运算法则。了解这些误用和错误有助于我们避免在求解问题时犯类似的错误。

如何有效使用根号符号解决数学问题

运算法则和特性后、掌握根号符号的基本概念、我们可以更有效地使用根号符号来解决数学问题。化简表达式以及理解根号的意义和应用等方面，运用根号运算法则，这包括合理选择被开方数。

根号符号的现实应用与意义

根号符号在现实生活中也有着诸多应用，除了在数学领域中的广泛应用外。解决物理问题等，根号符号可以帮助我们计算贷款的利息，评估风险投资的回报率。了解这些现实应用和意义可以帮助我们将数学知识与实际问题相结合。

根号符号的发展与拓展

随着数学的发展不断拓展和深化，根号符号作为一种数学符号。根号符号可以应用于微积分，在高级数学中，复变函数等领域。了解根号符号的发展和拓展可以帮助我们拓宽数学知识的边界。

结语：探索根号符号的无限魅力

我们更深入地了解了根号符号的意义、通过本文的探索，用途与运算法则。根号符号都扮演着重要的角色，无论是在数学领域中的应用，还是在现实生活中的实际问题求解中。并能在学习和应用中充分发挥其无限的魅力，希望读者能够通过本文的阐述、对根号符号有更加深入的认识。