直线对称的性质及应用（探索点关于直线对称的规律与应用）

直线对称是几何学中常见的一种性质，通过绕着一条直线旋转，可以使得平面上的点与其对称位置相互对应。本文将探讨直线对称的性质，以及它在几何中的应用。

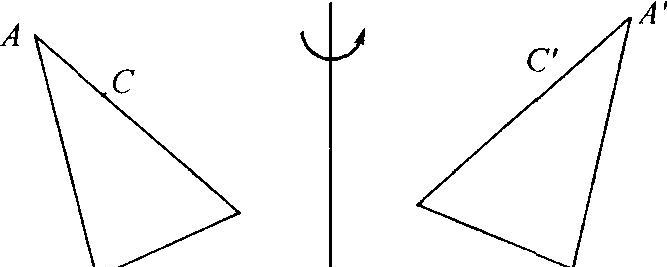
1.直线对称的定义和基本概念

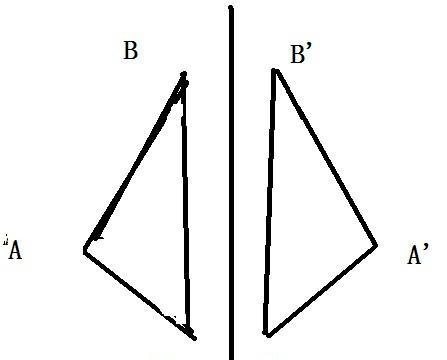
直线对称是指在平面上取一条直线，然后以该直线为轴将平面上的点进行旋转操作，使得每个点与其对称位置相互对应。

2.直线对称的特点与性质

直线对称具有保长度、保角度、保定向和保面积等特点，同时也满足可逆性和传递性的性质。

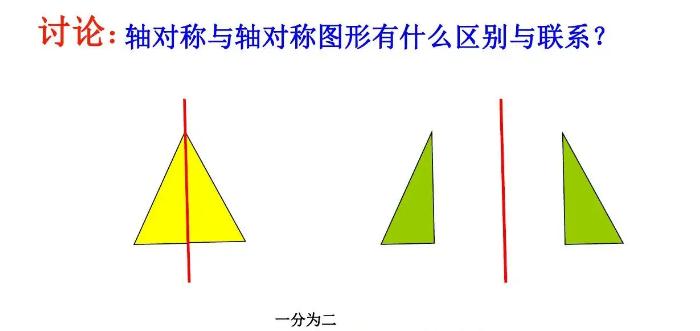
3.直线对称在图形判断中的应用

利用直线对称可以判断图形的对称性，从而简化判断过程，并帮助我们找到图形的重要特征和性质。

4.直线对称在图形构造中的应用

通过直线对称可以构造出各种图形，如等边三角形、正方形等，从而扩展了几何图形的种类和形态。

5.直线对称在数学建模中的应用

直线对称在数学建模中有着广泛的应用，例如在城市规划中用于确定建筑物的布局，或者在电路设计中用于优化电路的结构。

6.直线对称在自然界中的应用

自然界中存在着大量的直线对称现象，例如花朵、昆虫的身体结构等，这些都是基于直线对称性质而形成的。

7.直线对称在艺术中的应用

直线对称在艺术中常被用于构图和设计中，通过运用直线对称可以使作品更加美观和有吸引力。

8.直线对称与其他对称性质的关系

直线对称与点对称、中心对称等其他对称性质有着密切的联系和区别，通过比较可以更好地理解直线对称的特点。

9.直线对称与平移、旋转的关系

直线对称与平移、旋转是几何变换中常见的操作，它们之间存在着紧密的联系和相互作用。

10.直线对称在解题中的应用策略

在解决几何问题中，运用直线对称可以通过简化和转化问题来寻找解题的突破口和思路。

11.直线对称的数学证明

通过数学推理和证明可以得到直线对称的一些基本性质和结论，这为我们在应用中提供了理论支撑。

12.直线对称的计算方法与公式推导

根据直线对称的性质，可以推导出一些计算方法和公式，从而实现准确的计算和求解。

13.直线对称与实际问题的联系

直线对称不仅存在于几何学中，还与实际生活和科学问题有着紧密的联系，如物体运动、镜像成像等。

14.直线对称的扩展与应用领域

直线对称不仅仅局限于几何学，还可以扩展到其他学科和领域，如物理学、计算机图形学等。

15.直线对称的未来发展与研究方向

直线对称作为一种基本的几何性质，其未来的发展与研究将会涉及到更深入和广泛的领域，为我们提供更多的应用和探索空间。

直线对称作为几何学中重要的性质之一，具有丰富的特点和广泛的应用。通过研究直线对称的性质和应用，可以更好地理解几何图形的构成和变换规律，并在实际问题中应用几何知识来解决问题。同时，直线对称还与其他几何性质、数学建模、自然界、艺术和实际问题等领域有着密切的联系，为我们拓展了更广阔的学科视野和研究方向。